Det här läsåret läser jag och min närmaste kollega statliga Matematiklyftet vars syfte är att höja måluppfyllelsen i matematik genom att lyfta de lärare som undervisar i matematik. Arbetet är varierat mellan att å ena sidan läsa akademiska texter och å andra sidan planera, genomföra och utvärdera undervisning tillsammans med kollegor. Eftersom vi är en liten skola i en liten kommun så blir det att vi är lärare från tre skolor som arbetar tillsammans. Överlag är det en mycket intressant upplevelse som jag varmt rekommenderar.
Den här veckan genomför vi en serie undervisning kopplat till ett förutbetstämt problem som kallas ”Målade kuber” som vi hämtat från Problembanken.
Lotta har limmat ihop 27 likadana små kuber till en stor kub.
Sedan målar hon den stora kuben runt om på alla sidytor.
Hur många av de små kuberna har sedan
a) Tre sidor målade?
b) Två sidor målade?
c) En sida målad?
d) Ingen målad sida?
Vidare får elever i uppgift att jämföra hur det skulle förhålla sig om en byggde kuber som var större.
Under inläsningsfasen av det här momentet så får vi ta del av någon lärare som med videokamera filmat två elever som på papper löser problemet. Det är intressant, men känns suboptimalt eftersom det inte går att genomföra med 36 elever samtidigt. Så när uppgiften blir att försöka dokumentera elevernas parvisa arbete så landar jag i att byta videokamera och papper mot lärpaltta och appen Educreations. Det är en app som gör lärplattan till en inspelningsbar whiteboard, i princip. Direkt kan eleverna två och två både dokumentera och ”filma” sitt eget arbete utan att jag behöver finnas med för det tekniska. Istället blir mitt fokus undervisning och observation av lärande.
För att stärka upp har jag med mig en drös centimeterstora palstkuber som är gjorda för att sättas ihop, men som i ärlighetens namn är rätt pilliga. Så efter ett tag försvinner en ny elev iväg. Strax tillbaka har hen 27 tärningar som blir till en kub – allt för att visualisera själva problemet. Det är en smart och användbar lösning. Men att hålla sig till praktiskt material har flera stora begränsningar. Att bara rita gör det också onödigt svårt. Allt som allt är det nästan som om det är utmaningen med materialen som gör den här uppgiften till ett problem istälelt för en rutinuppgift.
Så när lektionen är slut och jag sitter med 18 elevpars inspelade lösningar så börjar mitt arbete att analysera. Snabbt blir det klart för mig att jag nästa dag borde följa upp och förklara. På det viset kan jag kompensera för faktumet att en del par lyckades knäcka nöten medans andra fastnade någonstans på vägen. Teknikvalet faller på iOS-versionen av Minecraft.
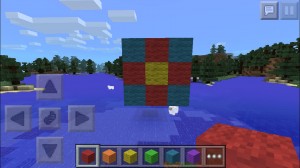
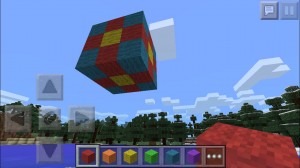
I det här sammanhanget väljer jag Minecraft eftersom det är ett enkelt verktyg för att simulera saker i 3D och eftersom jag har det nära till hands på skolans lärplattor.
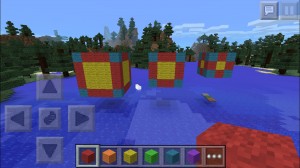
Jag kopplar upp mot projektorn och tar runt eleverna på en flygtur runt kuben jag byggt, för att räkna sidor och kolla på kuberna/blocken. Det är lätt att hacka bort, lägga till och byta ut. Det är också lätt att flyga en bit längre bort och kolla in de tre kuber i olika storlekar som jag byggt för att ge eleverna en chans att se hur vissa delar (de med två, en och noll sidor målade) ökar i takt med att kuben blir större medan hörnen fortfarande är lika många. Alla nickar och hänger med.
När vi nästa vecka återses i vår lilla lärargrupp för att utvärdera och dela erfarenheter så visar det sig att resultaten skiljer sig mer än någonsin förr. Det finns flera grupper där uppgiften har varit svår och där slutklämmen, att jämföra med större kuber, till och med uppfattas som löjeväckande svår. ”Den gör jag inte för det går ju inte att lösa” skrattar de. Men inte mina elever. De ser och förstår.
Och det här är inget speciellt. Det finns gott om forskning som ger stöd åt att elever skapar en annan förståelse av tredimensionella objekt när de får studera just tredimensionella modeller av dem. På ett sätt borde det vara en av de didaktiska frågor vi ställer oss inför undervisningen vi utsätter våra elever för.